What is a Higgs boson?

The discovery of the Higgs boson was a triumph for particle physics. Its discovery completes the tremendously successful Standard Model of particle physics. Of course, we know there are other phenomena — like dark matter, the dominance of matter over anti-matter, the mass of neutrinos, etc. — that aren’t explained by the Standard Model. However, the Higgs itself is the source of one of the deepest mysteries of particle physics: the fine tuning problem.

The fine-tuning problem is related to the slippery concept of naturalness, and has driven the bulk of theoretical work for the last several decades. Unfortunately, it is notoriously difficult to explain. I took on this topic recently for a public lecture and came up with an analogy that I would like to share.

Why we take our theory seriously

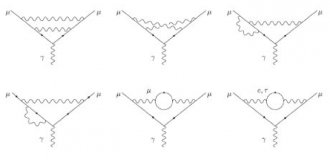
Before discussing the fine tuning, we need need a few prerequisites. The first thing to know is that the Standard Model (and most other theories we are testing) is based on a conceptual framework called Relativistic Quantum Field Theory (QFT). As you might guess from the name, it’s based on the pillars of relativity, quantum mechanics, and field theory. The key point here is that relativistic quantum field theory goes beyond the initial formulation of quantum mechanics. To illustrate this difference, let’s consider a property of the electron and muon called its “g-factor” that relates its magnetic moment and spin [more]. In standard quantum mechanics, the prediction is that g=2; however, with relativistic quantum field theory we expect corrections. Those corrections are shown pictorially in the Feynman diagrams below.

It turns out that this correction is small — about one part in a thousand. But we can calculate it to an exquisite accuracy (about ten digits). Moreover, we can measure it to a comparable accuracy. The current result for the muon is

g = 2. ± 0.000000001

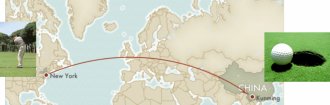
This is a real tour de force for relativistic quantum field theory and represents one of the most stringent tests of any theory in the history of science [more]. To put it into perspective, it’s slightly better than hitting a hole in one from New York to China (that distance is about 10, 000 km =1 billion cm).