Isaac Newton law of Gravitation

To calculate the force of gravity on the Moon, one must also know how much weaker it was at the Moon's distance. Newton showed that if gravity at a distance R was proportional to 1R2 (varied like the "inverse square of the distance"), then indeed the acceleration g measured at the Earth's surface would correctly predict the orbital period T of the Moon.

Newton went further and proposed that gravity was a "universal" force, and that the Sun's gravity was what held planets in their orbits. He was then able to show that Kepler's laws were a natural consequence of the "inverse squares law" and today all calculations of the orbits of planets and satellites follow in his footsteps.

Nowadays students who derive Kepler's laws from the "inverse-square law" use differential calculus, a mathematical tool in whose creation Newton had a large share. Interestingly, however, the proof which Newton published did not use calculus, but relied on intricate properties of ellipses and other conic sections. Richard Feynman, Nobel-prize winning maverick physicist, rederived such a proof (as have some distinguished predecessors); see reference at the end of the section.

Here we will retrace the calculation, which linked the gravity observed on Earth with the Moon's motion across the sky, two seemingly unrelated observations. If you want to check the calculation, a hand-held calculator is helpful.

Calculating the Moon's Motion

We assume that the Moon's orbit is a circle, and that the Earth's pull is always directed toward's the Earth's center. Let RE be the average radius of the Earth (first estimated by Erathosthenes)

RE= 6 371 km

The distance R to the Moon is then about 60 RE. If a mass on Earth is pulled by a force mg, and if Newton's "inverse square law" holds, then the pull on the same mass at the Moon's distance would be 602 = 3600 times weaker and would equal

mg3600

If is the mass of the Moon, that is the force which keeps the Moon in its orbit. If the Moon's orbit is a circle, since R = 60 RE its length is

2 π R = 120 π RE

Suppose the time required for one orbit is T seconds. The velocity v of the motion is then

v = distancetime = 120 π RET

(Please note: gravity is not what gives the Moon its velocity. Whatever velocity the Moon has was probably acquired when it was created. But gravity prevents the Moon from running away, and confines it to some orbit.)

The centripetal force holding the Moon in its orbit must therefore equal

mv2R = mv2(60 RE)

and if the Earth's gravity provides that force, then

mg3600 = mv2(60 RE)

dividing both sides by and then multiplying by 60 simplifies things to

g60 = v2RE = (120 π RE)2(T2 RE)

Canceling one factor of RE, multiplying both sides by 60 T2 and dividing them by g leaves

T2 = (864 000 π2 RE)g = 864 000 RE (π2g)

Providentially, in the units we use g ~ 9.81 is very close to π2 ~ 9.87, so that the term in parentheses is close to 1 and may be dropped. That leaves (the two parentheses are multiplied)

T2 = (864 000) (6 371 000)

With a hand held calculator, it is easy to find the square roots of the two terms. We get (to 4-figure accuracy)

864 000 = (929.5)2 6 371 000 = (2524)2

Then

T ≅ (929.5) (2524) = 2 346 058 seconds

To get T in days we divide by 86400, the number of seconds in a day, to get

T = 27.153 days

pretty close to the accepted value

T = 27.3217 days

The above looks like a simple and straightforward calculation. However, it assumes something we nowadays accept without second thought: that the pull of the Earth would be the same if all the mass of the Earth were concentrated in its center.
It wasn't obvious to Newton, That falling apple... sure, there was mass pulling it down, but there was also mass pulling it sideways in all directions, pulls which largely canceled. Even if the sum-total of all pulls pointed towards the center of the Earth, who was to say it obeyed the same inverse-square law as a mass concentrated at a point? Newton did not trust the above calculation until he proved to his satisfaction that the Earth's attraction could always be replaced by the one of a mass concentrated at its center.

Making a discovery often involves groping and guessing, before a clear pattern emerges. We, who know that pattern and take it for granted, may feel the discovery was obvious. But it need not have appeared at first.

The Formula for the Force of Gravity

Newton rightly saw this as a confirmation of the "inverse square law". He proposed that a "universal" force of gravitation F existed between any two masses m and M, directed from each to the other, proportional to each of them and inversely proportional to the square of their separation distance r. In a formula (ignoring for now the vector character of the force):

F = G mM/r2

Suppose M is the mass of the Earth, R its radius and m is the mass of some falling object near the Earth's surface. Then one may write

F = m GM/R2 = m g

From this

g = GM/R2

The capital G is known as the constant of universal gravitation. That is the number we need to know in order to calculate the gravitational attraction between, say, two spheres of 1 kilogram each. Unlike the attraction of the Earth, which has a huge mass M, such a force is quite small, and the number G is likewise very, very small. Measuring that small force in the lab is a delicate and difficult feat.

It took more than a century before it was first achieved. Only in 1796 did Newton's countryman Henry Cavendish actually measure such weak gravitational attraction, by noting the slight twist of a dumbbell suspended by a long thread, when on of its weights was attracted by the gravity of heavy objects. His instrument ("torsion balance") is actually very similar to the one devised in France by by Charles Augustin Coulomb to measure the distance dependence of magnetic and electric forces. The gravitational force is much weaker, however, making its direct observation much more challenging. A century later (as already noted) the Hungarian physicist Roland Eötvös greatly improved the accuracy of such measurements.

Gravity in our Galaxy (Optional)

Gravity obviously extends much further than the Moon. Newton himself showed the inverse-square law also explained Kepler's laws-for instance, the 3rd law, by which the motion of planets slows down, the further they are from the Sun.

What about still larger distances? The solar system belongs to the Milky Way galaxy, a huge wheel-like swirl of stars with a radius around 100, 000 light years. Being located in the wheel itself, we view it edge-on, so that the glow of its distant stars appears to us as a glowing ring circling the heavens, known since ancient times as the Milky Way. Many more distant galaxies are seen by telescopes, as far as one can see in any direction. Their light shows (by the "Doppler effect") that they are slowly rotating.

Gravity apparently holds galaxies together. At least our galaxy seems to have a huge black hole in its middle, a mass several million times that of our Sun, with gravity so intense that even light cannot escape it. Stars are much denser near the center of our galaxy, and their rotation near their center suggests Kepler's third law holds there, slower motion with increasing distance.

The rotation of galaxies away from their centers does not follow Kepler's 3rd law-indeed, outer fringes of galaxies seem to rotate almost uniformly. This observed fact has been attributed to invisible "dark matter" whose main attribute is mass and therefore, gravitational attraction (see link above). It does not seem to react to electromagnetic or nuclear forces, and scientists are still seeking more information about it.

Exploring Further

A detailed article: Keesing, R.G., The History of Newton's apple tree, Contemporary Physics, 39, 377-91, 1998

Richard Feynman's calculations can be found in the book "Feynman's Lost Lecture: The Motion of Planets Around the Sun" by D. L Goodstein and J. R. Goodstein (Norton, 1996; reviewed by Paul Murdin in Nature, vol. 380, p. 680, 25 April 1996). The calculation is also described and expanded in "On Feynman's analysis of the geometry of Keplerian orbits" by M. Kowen and H. Mathur, Amer. J. of Physics, by V. Kuznetsov. Quantum, Sept-Oct. 1999, p. 38-41.

Questions from Users: What is the gravity at the center of the Earth? (1)
Similar question: Gravity at the Center pf the Earth's (2)
Also asked: Can gravity increase with depth?.
*** Follow-up to above question
*** Why does gravity exist?
*** "Gravity Particles"?
*** Gravity at the Center of Earth (3)
*** A simple question about gravitational energy
*** Effect of Gravity on Electromagnetic Waves
*** The speed at which gravity spreads
*** Does the Sun overhead reduce effective weight?
*** Difference between Gravity and Magnetism

Source: www.phy6.org

INTERESTING VIDEO

Isaac Newton. Gravity Part 1 of 2

newtons law of gravity part 1

Isaac Newton’s First Law of Motion

INTERESTING FACTS

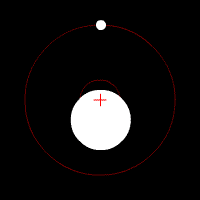Doppler spectroscopy, also known as radial velocity measurement, is a spectroscopic method for finding extrasolar planets. It involves the observation of Doppler shifts in the spectrum of the star around which the planet orbits.
It is extremely difficult to directly...
The first law of geography according to Waldo Tobler is "Everything is related to everything else, but near things are more related than distant things."
This observation is embedded in the gravity model of trip distribution. It is also related to the law of demand...
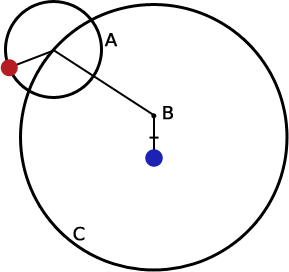In the Ptolemaic system of astronomy, the epicycle (literally: on the circle in Greek) was a geometric model used to explain the variations in speed and direction of the apparent motion of the Moon, Sun, and planets. It was first proposed by Apollonius of Perga at...