
This division is concerned with the unification of general relativity and quantum mechanics into a theory of quantum gravity, which should also provide a consistent framework for incorporating the other fundamental forces in nature.
Despite intense efforts over the last years it is far from clear at this time what a consistent theory of quantum gravity will look like and what its main features will be. In view of these uncertainties, the best strategy appears to be one which is both diversified and interdisciplinary. For this reason, the division aims to represent all the major current approaches to quantum gravity, in particular supergravity and string theory and their modern developments, as well as canonical quantization (e.g. loop quantum gravity) and discrete models of quantum gravity.
The canonical approaches to quantum gravity emphasize the geometrical aspects and appear well suited to deal with unsolved conceptual issues of quantum gravity, such as e.g. the problem of time or the interpretation of the wave function of the universe. Important new insights have been gained over the past decade in the framework of loop quantum gravity, whose modern variants (spin foam gravity and group field theory) are among the division's main research directions. This approach, which complements and extends the old geometrodynamics approach, employs a non-perturbative and background independent framework allowing (at least in principle) to describe the fluctuations of geometry itself, and leading to a discrete structure at the Planck scale. On this basis, it is now possible to study the full quantum dynamics of gravity and space-time itself. Most recently, these concepts have been successfully applied to the study of cosmological and black hole singularities, where classical general relativity breaks down. In this way it may become possible to understand how the Big Bang singularity of classical relativity is “dissolved” in quantum cosmology.
String theory, on the other hand, takes a very different point of departure in tackling the problem of quantum gravity. The requirement of mathematical consistency and the non-renormalizability of perturbatively quantized gravity, and the need to incorporate the non-gravitational interactions are likely to force us to modify Einstein's theory at the smallest distances (Planck scale). This may not only lead to a geometrization of the other fundamental forces (as exemplified by Kaluza-Klein theories and supergravity) and the unification of matter and gravity, but to an entirely new type of theory, which could explain how space-time is dissolved at very small distances, and in which Einstein's theory emerges only as an effective low energy theory, valid above distances above the Planck scale. Superstring and supermembrane theory, and supersymmetric matrix theory are the most promising ansaetze so far in this direction. Major progress in this area has been recently achieved by members of the division, in particular the framework of the so-called AdS/CFT correspondence, and the study of certain infinite dimensional symmetries, which might underlie a unified and non-perturbative description of string theory (M theory).
INTERESTING VIDEO



 Quantum gravity (QG) is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics (describing three of the four known fundamental interactions) with general relativity (describing the fourth, gravity). It is hoped that...
Quantum gravity (QG) is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics (describing three of the four known fundamental interactions) with general relativity (describing the fourth, gravity). It is hoped that...
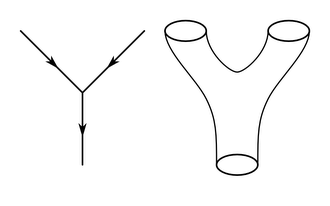 String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything (TOE), a self-contained mathematical model that describes all fundamental forces and...
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything (TOE), a self-contained mathematical model that describes all fundamental forces and...








